3 October 2023 by alevelmechanics1.com
Title: Braking Momentum: Deceleration Chronicles
Introduction: Embarking on a journey of braking dynamics, this numerical exploration delves into the scenario of a train hurtling at 80 m/s. When the driver commands a forceful deceleration, the train’s journey transforms, unraveling the intricacies of speed reduction and the spatial displacement during braking.
Scenario Overview: A high-speed train, barreling at 80 m/s, encounters a pivotal moment when the driver initiates a robust deceleration. The application of brakes introduces a significant alteration to the train’s velocity, prompting a detailed examination of its speed and the distance covered during this deceleration period.
Objective: Unravel the aftermath of braking as the train grapples with a deceleration force, determining the train’s speed after the braking episode and the total distance traversed during this dynamic maneuver.
Significance: This numerical exploration holds significance in understanding the consequences of abrupt deceleration on a fast-moving train, shedding light on both its velocity reduction and the spatial impact of braking.
Exploration Focus: The primary focus lies on calculating the train’s velocity post-braking and quantifying the total distance traveled during the deceleration interval.
Deceleration Chronicles: The journey unfolds in two stages: the initial breakneck speed of 80 m/s and the subsequent deceleration period. The train, subjected to a deceleration force of 2 m/s² for 30 seconds, experiences a significant transformation in both speed and displacement.
Mathematical Calculations: Leveraging kinematic equations, the train’s velocity after the deceleration episode is unveiled. Simultaneously, the total distance covered during the braking maneuver is quantified, offering a comprehensive insight into the train’s spatial displacement.
Visualization: Graphical representations may visually capture the evolving dynamics of speed and distance, providing a tangible depiction of the train’s response to the applied deceleration.
Douglas Quadling Mechanics 1
Exercise 1B Q6
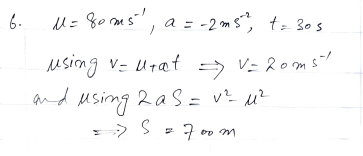
Conclusion:
As the train hurtles through its high-speed trajectory and encounters the decisive force of deceleration, this numerical exploration unveils the post-braking velocity and the cumulative distance covered during this transformative episode. The journey of braking dynamics encapsulates the dynamic interplay between speed reduction and spatial displacement, offering a glimpse into the intricacies of locomotive motion under the influence of applied forces.
CategoriesChapter 1, Exercise 1B
Leave a comment
Logged in as alevelmechanics1.com. Edit your profile. Log out? Required fields are marked *
