The Problem:
A car comes to a stop from a speed of 30 m s in a distance of 804 m. The driver brakes so as to produce a deceleration of m s2 to begin with, and then brakes harder to produce a deceleration of ms2. Find the speed of the car at the instant when the deceleration is increased, and the total time the car takes to stop.
:
Objectives:
Douglas Quadling Mechanics1 Exercise1D Q5
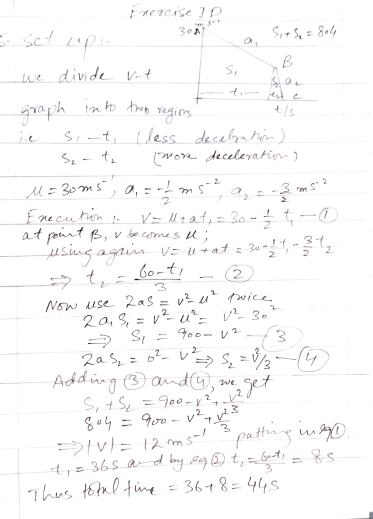
Solution:
Step 1: Define Variables
Given:
- Initial speed: u = 30 m/s
- Final speed: v = 0 m/s
- Total distance: s = 804 m
- Deceleration in first phase: a1 = 0.5 m/s²
- Deceleration in second phase: a2 = 1.5 m/s²
- Distance covered in first phase: s1
- Distance covered in second phase: s2
Since the total stopping distance is 804 m:
s1 + s2 = 804
Step 2: Finding the Speed When Deceleration Increases
Using the equation of motion:
v² = u² + 2a1s1
v² = (30)² + 2 × (-0.5) × s1
v² = 900 – s1
For the second phase:
0² = v² + 2a2s2
0 = v² + 2 × (-1.5) × s2
s2 = v² / 3
Since s1 + s2 = 804, we substitute:
s1 + (900 – s1)/3 = 804
Multiplying by 3:
3s1 + 900 – s1 = 2412
2s1 = 1512
s1 = 756, s2 = 804 – 756 = 48
Now using v² = 900 – s1:
v² = 900 – 756 = 144
v = 12 m/s
Step 3: Finding the Time for Each Phase
First Phase (0.5 m/s² deceleration)
Using v = u + at:
12 = 30 – 0.5t1
0.5t1 = 18
t1 = 36 s
Second Phase (1.5 m/s² deceleration)
Using v = u + at:
0 = 12 – 1.5t2
1.5t2 = 12
t2 = 8 s
Step 4: Total Time
t_total = t1 + t2 = 36 + 8 = 44 s
Final Answers:
- The speed of the car when the deceleration increases is 12 m/s.
- The total time to stop is 44 seconds.