The Problem:
A car rounds a bend at 10 ms^-1, and then accelerates at 1/2ms^-2 along a straight stretch of road. There is a junction 400 m from the bend. When the car is 100 m from the junction, the driver brakes and brings the car to rest at the junction with constant deceleration. Draw a (t,v) graph to illustrate the motion of the car. Find how fast the car is moving when the brakes are applied, and the deceleration needed for the car to stop at the junction.
Douglas Quadling Mechanics1 Exercise1D Q4
A car rounds a bend at 10 ms^-1, and then accelerates at 1/2ms^-2 along a straight stretch of road. There is a junction 400 m from the bend……..
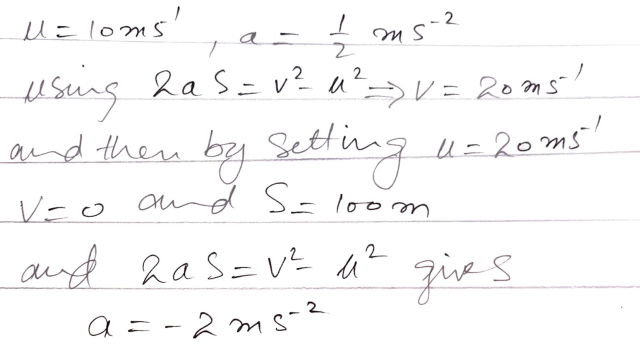
Solution:
Step 1: Finding the Speed When Brakes Are Applied
Using the equation of motion:
v² = u² + 2as
where:
- u = 10 m/s (initial speed)
- a = 0.5 m/s²
- s = 300 m
- v = final speed before braking
v² = (10)² + 2 × 0.5 × 300
v² = 100 + 300 = 400
v = 20 m/s
Step 2: Finding the Deceleration
Using the equation of motion again:
0 = v² + 2as
0 = (20)² + 2 × a × 100
0 = 400 + 200a
a = -2 m/s²
Step 3: Finding Time for Each Phase
Acceleration Phase:
Using v = u + at
20 = 10 + 0.5t
10 = 0.5t
t = 20 s
Braking Phase:
Using v = u + at
0 = 20 – 2t
2t = 20
t = 10 s
Step 4: Velocity-Time Graph
The graph consists of:
- A straight-line rise from 10 m/s to 20 m/s over 20 s.
- A straight-line fall from 20 m/s to 0 m/s over 10 s.
You can visualize the graph by plotting these points on a velocity-time plane.