The Problem:
A man is running for a bus at 3 m/ s. When he is 100 m from the bus stop, the bus passes him going at 8 m /s If the deceleration of the bus is constant, at what constant rate should the man accelerate so as to arrive at the bus stop at the same instant as the bus?
Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q9
A man is running for a bus at 3 m s. When he is 100 m from the bus stop, the bus passes him going at 8 m s1…..
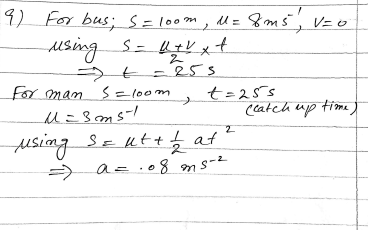
Given:
- Man’s initial speed: 3 m/s
- Distance to the bus stop: 100 m
- Bus’s initial speed: 8 m/s
- Bus’s deceleration: constant (unknown)
- Man’s acceleration: constant (to be determined)
Step 1: Time for the bus to reach the bus stop
The bus is decelerating, so its motion is described by:
Distance = (Initial Speed × Time) – (0.5 × Deceleration × Time²)
At the bus stop, the bus’s final speed is 0 m/s. Using the equation:
Final Speed = Initial Speed – (Deceleration × Time)
Substitute the values:
0 = 8 – (Deceleration × Time)
This gives:
Deceleration = 8 / Time
Substitute this into the distance equation:
100 = 8 × Time – 0.5 × (8 / Time) × Time²
Simplify:
100 = 8 × Time – 4 × Time
100 = 4 × Time
Time = 25 seconds
Step 2: Time for the man to reach the bus stop
The man is accelerating, so his motion is described by:
Distance = (Initial Speed × Time) + (0.5 × Acceleration × Time²)
Substitute the values:
100 = 3 × 25 + 0.5 × Acceleration × 25²
Simplify:
100 = 75 + 0.5 × Acceleration × 625
100 – 75 = 0.5 × 625 × Acceleration
25 = 312.5 × Acceleration
Acceleration = 25 / 312.5
Acceleration = 0.08 m/s²
Final Answer:
The man must accelerate at a constant rate of 0.08 m/s² to arrive at the bus stop at the same time as the bus.