The Problem:
A car is waiting at traffic lights with a van behind it. There is a 1 metre gap between them. When the lights turn green, the car accelerates at 1.5 ms-2 until it reaches a speed of 15 m/s; it then proceeds at this speed. The van does the same, starting when the gap between the vehicles is 4 metres. Find a formula for the distance travelled by the car in the first seconds (0≤t≤10), and hence the time interval between the car starting and the van starting. Find also the distance between the vehicles when they are both going at 15 m /s. (OCR)
Solution: A car is waiting at traffic lights with a van behind it. There is a 1 metre gap between them……..

Motion of Car and Van
Given Data:
Car:
- Initial speed, u = 0 m/s
- Acceleration, a = 1.5 m/s²
- Final speed, v = 15 m/s
- Accelerates for 10 seconds
- Then moves at constant velocity for 2 seconds
Van:
- Initial speed, u = 0 m/s
- Acceleration, a = 1.5 m/s²
- Starts moving 2 seconds after the car
- Accelerates for 10 seconds
Initial Gap: 1 meter
The van starts when the gap increases to 4 meters, so the car must travel 3 meters before the van starts.
Step 1: Distance Traveled by the Car
(a) Distance During Acceleration (First 10 seconds)
Using the equation: s = ut + (1/2) a t²
Since u = 0:
s = (1/2) × 1.5 × (10)²
s = 0.75 × 100
s = 75 m
(b) Distance During Constant Velocity (Last 2 seconds)
Using s = vt:
s = 15 × 2
s = 30 m
Total distance traveled by the car in 12 seconds:
75 + 30 = 105 m
Step 2: Distance Traveled by the Van in 10 Seconds
Since the van accelerates for 10 seconds:
s = ut + (1/2) a t²
s = (1/2) × 1.5 × (10)²
s = 75 m
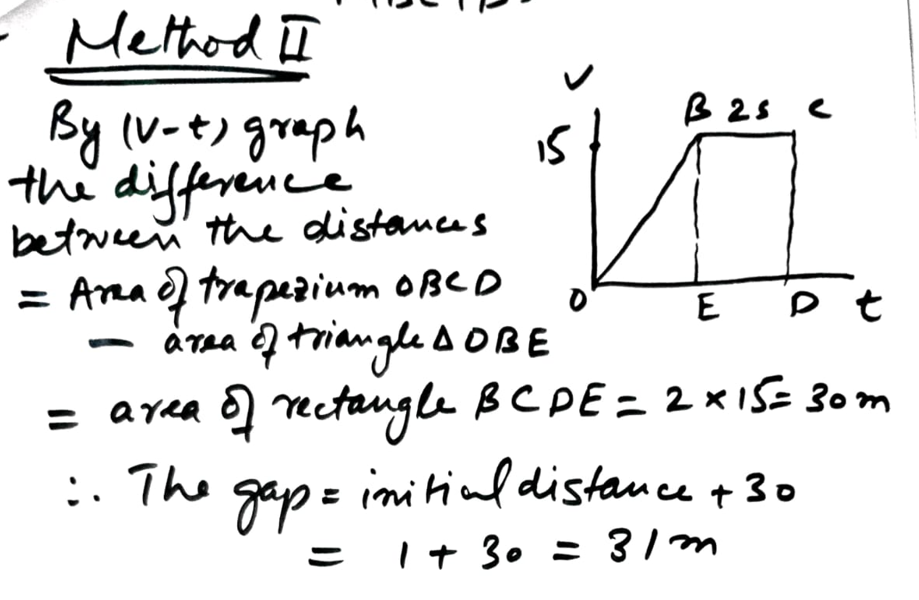
Step 3: Final Distance Between Car and Van
The car traveled 105 meters, and the van traveled 75 meters. Considering the initial 1-meter gap:
Final gap = 105 – 75 + 1 = 31 meters
Final Answers:
- Formula for the car’s distance:
- Time interval between car and van starting: 2 seconds
- Final distance between them when both reach 15 m/s: 31 meters
s = 0.75 t² for 0 ≤ t ≤ 10
s = 75 + 15(t – 10) for 10 ≤ t ≤ 12