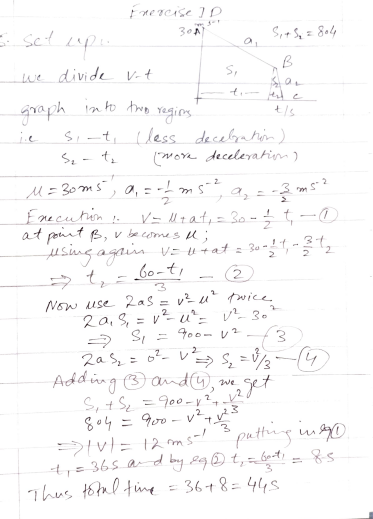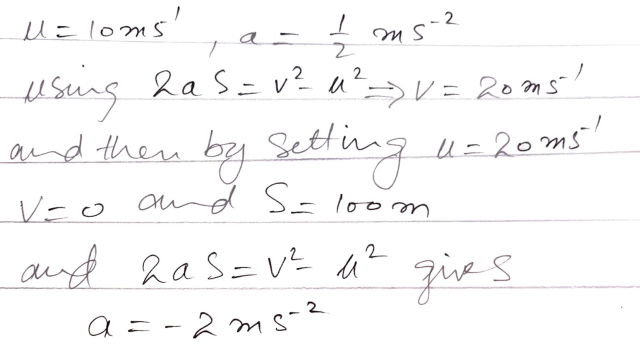A particle is moving along a straight line with constant acceleration. In an interval of T seconds it moves D metres; in the next interval of 3T seconds it moves 9D metres. How far does it move in a further interval of T seconds?
A particle is moving along a straight line with constant acceleration. In an interval of T seconds it moves D metres; in the next interval of 3T seconds it moves 9D metres.