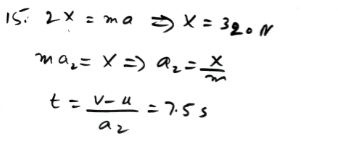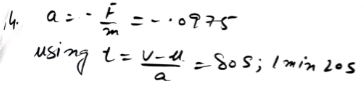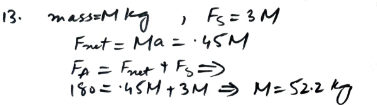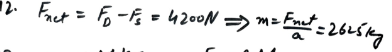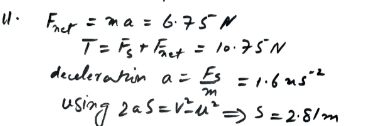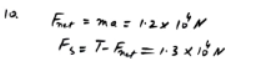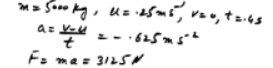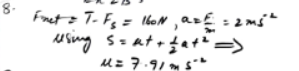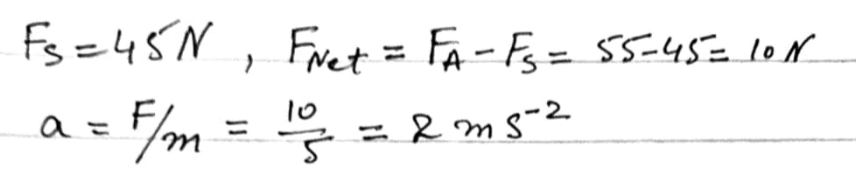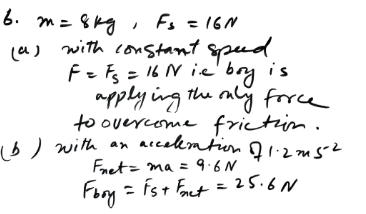Exercise 2B

One horse pulls, with a force of X N, a cart of mass 800 kg along a horizontal road at constant speed. Three horses, each pulling with a force of X N, give the cart an acceleration of 0.8 m s. Find the time it would take two horses to increase the speed of the cart from 2 m s1 to 5 ms, given that each horse pulls with a force of X N, and that the resistance to motion has the same constant value at all times.

by
Douglas Quadling Mechanics Exercise2B Q15

Douglas Quadling Mechanics1 Exercise2B Q15 one-horse-pulls-with-a-force-of-x-n-a-cart-of-mass-800-kg-along-a-horizontal-road-at-constant-speed-three-horses-each

A motor-boat of mass 8 tonnes is travelling along a straight course with a constant speed of 28 km h1. The constant force driving the boat forward has magnitude 780 N. Find the force resisting motion, assumed constant. The engine is now shut off. Calculate, to the nearest second, the time it takes the motor-boat to stop, assuming that the resistance remains the same as before.

by
Douglas Quadling Exercise 2B Q14 -motorboat- resisting force-time

Introduction: In the given numerical scenario, we are presented with a motorboat of mass 8 tonnes moving along a straight course at a constant speed of 28 km/h. The boat is subjected to a constant forward force with a magnitude of 780 N. The primary objective is to determine the force resisting the motion, assumed … Read more

A porter is pushing a heavy crate of mass M kg along a horizontal floor with a horizontal force of 180 N. The resistance to motion has magnitude 3M newtons. Given that the acceleration of the crate is 0.45 m s2, find the value of M.

by
Douglas Quadling Mechanics1 Exercise2B

A porter is pushing Introduction: A porter is pushing In the presented numerical scenario, a porter exerts a horizontal force of 180 N to push a heavy crate along a horizontal floor. The crate has a mass denoted as M kg, and it encounters a resistance to motion with a magnitude of 3M newtons. The … Read more

A particle of mass 2.5 kg is pulled along a horizontal surface by a string parallel to the surface with an acceleration of 2.7 ms. Given that the frictional force resisting motion has magnitude 4 N, calculate the tension in the string. At the instant that the particle is moving with speed 3 ms, the string breaks. Calculate how much further the particle moves before coming to rest.

by
image-26

A particle of mass 2.5 kg is pulled along a horizontal surface by a string parallel to the surface with an acceleration of 2.7 ms.

A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s, find the force, assumed constant, exerted on the engine by the buffers.

by
A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s, find the force, assumed constant, exerted on the engine by the buffers.

A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s, find the force, assumed constant, exerted on the engine by the buffers.

A water-skier of mass 80 kg is towed over a straight 100-metre run of water. The tension in the horizontal towline is constant and of magnitude 300 N. The resistance to motion of the skier has magnitude 140 N. Given that the skier takes 6.8 seconds to complete the run, calculate her speed at the start of the run.

by
A water-skier of mass 80 kg is towed over a straight 100-metre run of water. The tension in the horizontal towline is constant and of magnitude 300 N. The resistance to motion of the skier has magnitude 140 N. Given that the skier takes 6.8 seconds to complete the run, calculate her speed at the start of the run.

A water-skier of mass 80 kg is towed over a straight 100-metre run of water. The tension in the horizontal towline is constant and of magnitude 300 N. The resistance to motion of the skier has magnitude 140 N. Given that the skier takes 6.8 seconds to complete the run, calculate her speed at the start of the run.

A particle of mass 5 kg is pulled, with constant speed, along a rough surface by a horizontal force of magnitude 45 N. Calculate the magnitude of the frictional force. Assuming that this force remains constant, calculate the acceleration of the particle when the magnitude of the horizontal force is increased to 55 N.

by
A particle of mass 5 kg is pulled, with constant speed, along a rough surface by a horizontal force of magnitude 45 N. Calculate the magnitude of the frictional force.

A particle of mass 5 kg is pulled, with constant speed, along a rough surface by a horizontal force of magnitude 45 N. Calculate the magnitude of the frictional force. Assuming that this force remains constant, calculate the acceleration of the particle when the magnitude of the horizontal force is increased to 55 N.

A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N. Calculate the force with which the boy is pushing when he is moving. (a) with constant speed, (b) with a constant acceleration of 1.2 ms-2.

by
A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N.

A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N. Calculate the force with which the boy is pushing when he is moving. (a) with constant speed, (b) with a constant acceleration of 1.2 ms-2.