A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m. The speed of the cyclist at A is 8 ms and at B is 12 m s. Find the speed of the cyclist at C. (OCR)
Title: Cyclist’s Accelerated Journey: Speed Dynamics: A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m…….
Scope: Unveiling Acceleration Effects on Speed Along a Straight Road
1. Introduction : A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m….
- The journey of a cyclist unfolds along a straight road, marked by three pivotal points A, B, and C. This exploration delves into the cyclist’s constant acceleration and its impact on speed, with a particular focus on determining the speed of the cyclist at the third point, C.
2. Scenario Description:
- The cyclist’s journey is delineated by three significant points, A, B, and C, with equal distances AB and BC. The cyclist’s speed at the initial point A is known, and the speed at point B is provided. The objective is to unveil the speed of the cyclist at the third point, C, considering the constant acceleration along the straight road.
3. Objectives:
- The primary objective is to determine the speed of the cyclist at point C, leveraging the known speeds at points A and B, and considering the equal distances between these points.
4. Significance:
- The significance lies in unraveling the impact of constant acceleration on the cyclist’s speed, showcasing how the journey’s dynamics influence the velocity at each point along the straight road.
5. Exploration Focus:
- The exploration centers on understanding the implications of constant acceleration on speed, visualizing the cyclist’s journey, and employing mathematical calculations to ascertain the speed at point C.
6. Dynamics of Acceleration:
- Core dynamics involve analyzing the cyclist’s journey, emphasizing the constant acceleration experienced along the straight road, and deducing its effects on speed at different points.
7. Known Speeds at A and B:
- Analysis includes leveraging the known speeds at points A and B to establish a foundation for determining the speed at point C, considering the equal distances AB and BC.
8. Mathematical Calculations:
- The exploration incorporates mathematical calculations, potentially utilizing equations of motion, to derive the speed of the cyclist at point C based on the provided information.
Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q3
A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m.
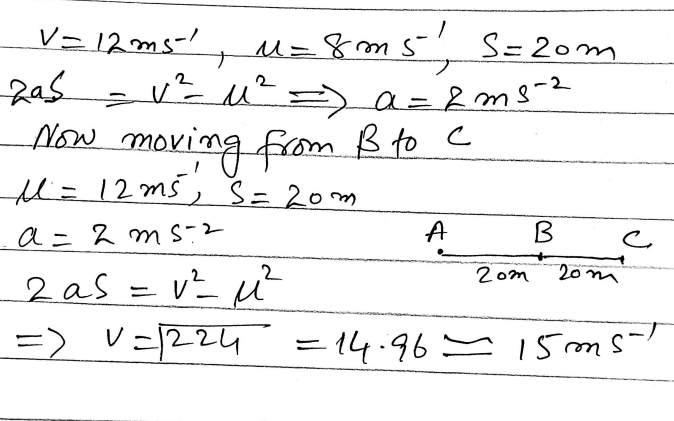
Visualization:
- Visualization plays a key role in comprehending the cyclist’s journey, and graphical representation may aid in illustrating the changing speeds at points A, B, and C.
Conclusion:
A cyclist, travelling with constant acceleration along a straight road, passes three points A, B and C, where AB = BC= 20 m…
- The exploration promises to reveal the speed of the cyclist at point C, offering insights into how constant acceleration shapes the dynamics of speed along the straight road and showcasing the calculated effects of the cyclist’s journey.