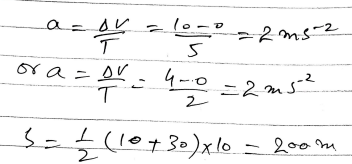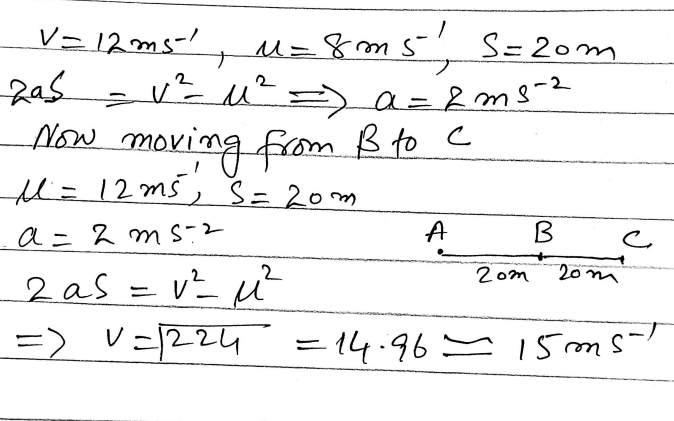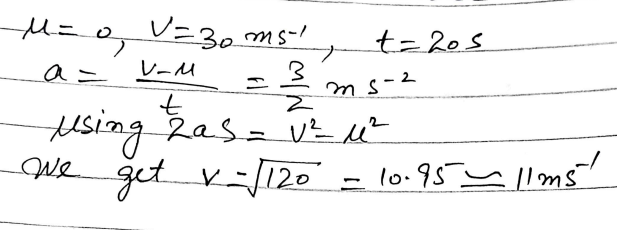alevelmechanics1.com

Two runners, Ayesha and Fatima, are leading the field in a long-distance race. They are both running at 5 ms, with Ayesha 10 m behind Fatima. When Fatima is 50 m from the tape, Ayesha accelerates but Fatima doesn’t. What is the least acceleration Ayesha must produce to overtake Fatima? If instead Fatima accelerates at 0.1 m s2 up to the tape, what is the least acceleration Ayesha must produce?

by
Two runners, Ayesha and Fatima, are leading the field in a long-distance race. They are both running at 5 ms, with Ayesha 10 m behind Fatima.

Two runners, Ayesha and Fatima, are leading the field in a long-distance race. They are both running at 5 ms, with Ayesha 10 m behind Fatima.

A car is waiting at traffic lights with a van behind it. There is a 1 metre gap between them. When the lights turn green, the car accelerates at 1.5 ms-2 until it reaches a speed of 15 m/s; it then proceeds at this speed. The van does the same, starting when the gap between the vehicles is 4 metres. Find a formula for the distance travelled by the car in the first seconds (0≤t≤10), and hence the time interval between the car starting and the van starting. Find also the distance between the vehicles when they are both going at 15 m /s. (OCR)

by
A car is waiting at traffic lights with a van behind it. There is a 1 metre gap between them.

A car is waiting at traffic lights with a van behind it. There is a 1 metre gap between them.

As a car passes the point A on a straight road, its speed is 10 m s. The car moves with constant acceleration am s2 along the road for T seconds until it reaches the point B, where its speed is V m s1. The car travels at this speed for a further 10 seconds, when it reaches the point C. From C it travels for a further T seconds with constant acceleration 3a ms2 until it reaches a speed of 20 m s1 at the point D. Sketch the (r,v) graph for the motion, and show that V = 12.5. Given that the distance between A and D is 675 m, find the values of a and T. (OCR)

by
As a car passes the point A on a straight road, its speed is 10 m s.

As a car passes the point A on a straight road, its speed is 10 m s.

A motorist travelling at u ms^-1 joins a straight motorway. On the motorway she travels with a constant acceleration of 0.07 m s2 until her speed has increased by 2.8 m s1. (a) Calculate the time taken for this increase in speed. (b) Given that the distance travelled while this increase takes place is 1050 m, find u. (OCR)

by
A motorist travelling at u ms^-1 joins a straight motorway. On the motorway she travels with a constant acceleration of 0.07 m s2 until her speed has increased by 2.8 m s1.

A motorist travelling at u ms^-1 joins a straight motorway. On the motorway she travels with a constant acceleration of 0.07 m s2 until her speed has increased by 2.8 m s1.

A car starts from rest at the point A and moves in a straight line with constant acceleration for 20 seconds until it reaches the point B. The speed of the car at B is 30 m s. Calculate (a) the acceleration of the car, (b) the speed of the car as it passes the point C, where C is between A and B and AC = 40 m. (OCR)

by
A car starts from rest at the point A and moves in a straight line with constant acceleration for 20 seconds until it reaches the point B.

A car starts from rest at the point A and moves in a straight line with constant acceleration for 20 seconds until it reaches the point B.

A train is slowing down with constant deceleration. It passes a signal at A, and after successive intervals of 40 seconds it passes points B and C, where AB = 1800 m and BC= 1400 m. (a) How fast is the train moving when it passes A? (b) How far from A does it come to a stop?

by
A train is slowing down with constant deceleration. It passes a signal at A, and after successive intervals of 40 seconds it passes points B and C, where AB = 1800 m and BC= 1400 m.

A train is slowing down with constant deceleration. It passes a signal at A, and after successive intervals of 40 seconds it passes points B and C, where AB = 1800 m and BC= 1400 m.

A roller-skater increases speed from 4 m/s to 10 ms in 10 seconds at a constant rate. (a) What is her average velocity over this period? (b) For what proportion of the time is she moving at less than her average velocity? (c) For what proportion of the distance is she moving at less than her average velocity?

by
A roller-skater increases speed from 4 m/s to 10 ms in 10 seconds at a constant rate. (a) What is her average velocity over this period?

A roller-skater increases speed from 4 m/s to 10 ms in 10 seconds at a constant rate. (a) What is her average velocity over this period?