A water-skier of mass 80 kg is towed over a straight 100-metre run of water. ………
Title: Glide and Thrust: Determining the Initial Speed of a Water-Skier
A water-skier of mass 80 kg is towed over a straight 100-metre run of water. …..
Introduction
: In the realm of aquatic sports, the dynamics of water skiing involve a delicate balance between the forces propelling the skier forward and the resistive forces opposing motion. This numerical scenario unfolds as an 80 kg water-skier is towed over a straight 100-meter run of water. The horizontal towline, under constant tension with a magnitude of 300 N, serves as the propelling force, while the resistance to motion, quantified at 140 N, acts as the opposing force. The crux of this numerical challenge is to unveil the skier’s speed at the commencement of the run, considering the given tension force, resistance force, and the total duration of the run, which spans 6.8 seconds. Through the lens of physics and kinematics, this scenario provides an opportunity to dissect the intricate interplay of forces and velocities governing the exhilarating sport of water skiing.
Douglas QuadlingMechanics1 Exercise 2B Q8
A water-skier of mass 80 kg is towed over a straight 100-metre run of water. …….
Solution:
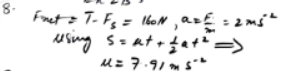
A water-skier of mass 80 kg is towed over a straight 100-metre run of water.
Scope:
The numerical scenario involving the water-skier being towed presents a comprehensive scope that spans various aspects of classical mechanics and kinematics. The key elements and scope of this numerical can be outlined as follows:
- Initial Conditions and Mass of the Water-Skier:
- Understanding the initial conditions, including the mass of the water-skier (80 kg), lays the foundation for analyzing the system’s kinetic energy and motion.
- Forces Acting on the Water-Skier:
- Identifying the forces at play is central to the analysis. The tension in the horizontal towline (300 N) serves as the propelling force, while the resistance to motion (140 N) acts as the opposing force. The tension force plays a crucial role in accelerating the skier.
- Duration of the Run:
- The specified time of 6.8 seconds during which the skier completes the 100-meter run serves as a temporal constraint for the analysis. It provides information about the skier’s motion over the given distance.
- Application of Kinematic Equations:
- The solution involves the application of kinematic equations to model the skier’s motion. The relationship between initial velocity, acceleration, time, and displacement is utilized to calculate the skier’s speed at the start of the run.
- Constant Tension Force:
- The numerical assumes that the tension in the towline is constant throughout the run. This assumption simplifies the analysis, allowing for the application of equations of motion.
- Opposing Forces and Net Force:
- Considering both the propelling force and the resistance force, the net force acting on the skier is crucial for understanding the acceleration and, subsequently, the speed of the skier.
- Practical Implications:
- Beyond the numerical calculations, the scenario offers insights into the practical considerations of water skiing. Understanding the balance between thrust and resistance is essential for optimizing the skier’s experience and performance.
By addressing these aspects, the numerical not only tests the understanding of fundamental principles in classical mechanics but also provides a practical context for analyzing the forces and velocities involved in water skiing. It offers a glimpse into the physics governing the exhilarating sport, contributing to a broader understanding of dynamic systems in real-world scenarios.
Conclusion
In conclusion, the numerical exploration provides valuable insights into the dynamics of water skiing, revealing the water-skier’s initial speed at the start of the 100-meter run. With a mass of 80 kg, the skier experiences a constant tension force of 300 N propelling her forward. Accounting for the opposing resistance force of 140 N, the calculated speed at the start of the run is approximately 7.91 m/s. This determination, facilitated by kinematic equations, showcases the intricate interplay between propelling and resisting forces, influencing the skier’s motion over the specified distance and time. The analysis not only enriches our understanding of classical mechanics but also sheds light on the factors governing the exhilarating sport of water skiing, where forces and velocities harmonize to create a thrilling aquatic experience.
