A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N……
Title: Dynamics in Motion: Calculating Force in Box Pushing Scenarios
Introduction:
A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N……..
The scenario of a boy pushing a box of old newspapers unfolds a classic example of applied physics in daily life. As the boy exerts horizontal force against the box’s mass of 8 kg, a frictional force of 16 N opposes the motion. The central focus of this numerical challenge is to calculate the force applied by the boy under two distinct conditions: (a) when the box moves with a constant speed, and (b) when the box undergoes a constant acceleration of 1.2 m/s². This exploration delves into the dynamics of forces, equilibrium, and acceleration, providing a practical perspective on the interplay between applied force and friction in scenarios commonly encountered in our everyday experiences.
Solution:
A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N.
Douglas Quadling Mechanics1 Exercise 2B Q6
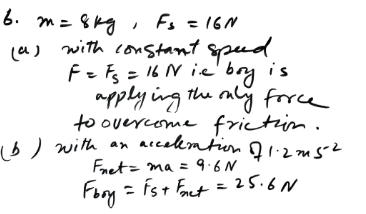
Scope
A boy is pushing, horizontally, a box of old newspapers of mass 8 kg along a straight path, against a frictional force of 16 N……
The numerical scenario involving the boy pushing a box of old newspapers presents a comprehensive scope that involves various aspects of classical mechanics and dynamics. The key elements and scope of this numerical can be outlined as follows:
- Static Equilibrium Analysis:
- The scenario begins with the boy pushing the box against a static frictional force. Calculating the force applied when the box is moving with constant speed involves understanding the equilibrium of forces and overcoming static friction.
- Constant Speed Motion:
- Analyzing the forces acting on the box when moving at a constant speed is crucial. This includes determining the force applied by the boy, balancing it with the opposing frictional force, and achieving a net force of zero during uniform motion.
- Dynamic Equilibrium and Constant Acceleration:
- Transitioning to the second part of the scenario, the analysis involves determining the force applied by the boy when the box is subjected to a constant acceleration of 1.2 m/s². This requires applying Newton’s second law to account for the acceleration and the frictional force.
- Application of Newton’s Laws:
- The solution relies on the application of Newton’s laws of motion, specifically focusing on the relationship between force, mass, and acceleration. This enables the calculation of the force exerted by the boy in both scenarios.
- Frictional Force Consideration:
- Understanding and accounting for the frictional force of 16 N opposing the motion is integral to the analysis. The force applied by the boy must overcome this resistance to initiate and maintain motion.
- Real-world Application:
- Beyond the numerical calculations, the scenario reflects a common real-world situation where individuals exert force to move objects against friction. The analysis provides practical insights into the physics of everyday actions.
- Concepts of Equilibrium and Acceleration:
- The numerical problem integrates concepts of static and dynamic equilibrium, emphasizing the interplay of forces during both constant speed motion and constant acceleration.
By addressing these aspects, the numerical not only tests the understanding of fundamental principles in classical mechanics but also provides a practical context for analyzing forces and accelerations in scenarios commonly encountered in daily life. It highlights the importance of overcoming frictional resistance and achieving equilibrium for smooth motion and acceleration
Conclusion
In conclusion, the numerical analysis unravels the dynamics of a boy pushing a box against a frictional force, shedding light on the force exerted under two distinct scenarios. When moving with constant speed, the calculated force is found to be equal and opposite to the frictional force, maintaining equilibrium during uniform motion. Transitioning to the second scenario, where the box undergoes a constant acceleration of 1.2 m/s², the boy’s applied force surpasses the frictional resistance, resulting in acceleration. This exploration not only emphasizes the application of Newton’s laws but also underscores the practical significance of overcoming frictional forces in real-world scenarios. The dual perspectives offered — one capturing static equilibrium and the other dynamic acceleration — showcase the nuanced interplay of forces encountered in the physical world, providing valuable insights into the physics of everyday actions.
