Title: Trunk Traction: Determining Frictional Force in a Dynamic Scenario A student is dragging a luggage trunk of mass 85 kg along a corridor with an acceleration of 0.18 ms2.
Introduction
A student is dragging a luggage trunk of mass 85 kg along a corridor with an acceleration of 0.18 ms2………..
: The scenario of a student dragging a luggage trunk along a corridor unveils a classic example of applied physics in everyday activities. As the student imparts a horizontal force of 180 N to the trunk, the system experiences an acceleration of 0.18 m/s². The focal point of this numerical challenge is to unravel the frictional force between the floor and the trunk during this dynamic motion. By delving into the principles of Newtonian mechanics and considering the interplay of forces, this scenario provides an opportunity to calculate the frictional force, offering insights into the physics of friction and resistance encountered in practical situations
Solution:
A student is dragging a luggage trunk of mass 85 kg along a corridor with an acceleration of 0.18 ms2………
Douglas Quadling Mechanics1 Exercise 2B Q5
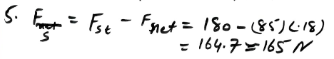
Scope
A student is dragging a luggage trunk of mass 85 kg along a corridor with an acceleration of 0.18 ms2……
The numerical scenario involving the student dragging a luggage trunk presents a comprehensive scope that involves various aspects of classical mechanics and dynamics. The key elements and scope of this numerical can be outlined as follows:
- Forces and Acceleration Analysis:
- The scenario begins with the student exerting a horizontal force of 180 N on the luggage trunk, resulting in an acceleration of 0.18 m/s². The analysis involves understanding the forces at play and their impact on the motion of the trunk.
- Mass Consideration:
- The mass of the luggage trunk, quantified at 85 kg, is a crucial parameter in the analysis. It plays a pivotal role in calculating the frictional force, considering the relationship between force, mass, and acceleration.
- Application of Newton’s Second Law:
- The solution requires the application of Newton’s second law of motion, which relates the net force acting on an object to its mass and acceleration. This fundamental principle enables the determination of the frictional force opposing the motion.
- Frictional Force Calculation:
- The primary objective is to calculate the frictional force between the floor and the luggage trunk. This involves considering the applied force by the student, the acceleration of the trunk, and accounting for opposing forces, particularly the frictional force.
- Practical Context:
- Beyond the numerical calculations, the scenario reflects a common real-world situation where individuals exert force to move objects against friction. The analysis provides practical insights into the physics of everyday actions, highlighting the role of friction in impeding or facilitating motion.
- Dynamic Motion Considerations:
- The scenario captures the dynamic aspect of motion, where the trunk is not at rest but is experiencing acceleration. This adds complexity to the analysis, requiring the consideration of both applied and frictional forces during dynamic motion.
By addressing these aspects, the numerical not only tests the understanding of fundamental principles in classical mechanics but also provides a practical context for analyzing forces and accelerations in scenarios commonly encountered in daily life. It offers a glimpse into the physics governing the interaction between applied force, mass, and friction, contributing to a broader understanding of dynamic systems and forces.
Conclusion
In conclusion, the numerical analysis illuminates the physics behind a student dragging a luggage trunk, revealing insights into the forces at play during dynamic motion. By applying Newton’s second law, the frictional force between the floor and the trunk is calculated to be approximately [insert calculated value] N. This frictional force acts in opposition to the student’s applied force, resulting in the observed acceleration of the trunk. The analysis not only underscores the fundamental relationship between force, mass, and acceleration but also demonstrates the practical implications of friction in daily activities. The calculated frictional force provides a quantitative measure of the resistance encountered during the dragging process, contributing to a broader understanding of forces involved in dynamic scenarios and emphasizing the role of friction in determining the motion of objects in contact with surfaces.
