Title: Dynamic Deceleration: Determining Resistance Force in Particle Motion A particle P of mass m kg is moving in a straight line with constant deceleration……….
In the realm of particle dynamics, our numerical exploration focuses on the trajectory of a particle, denoted as P, moving along a straight line with a consistent deceleration. This particle gracefully passes through two distinct points, A and B, with speeds of 6 m/s6m/s and 3.6 m/s3.6m/s, respectively. The intriguing facet of this scenario lies in unraveling the force that staunchly resists the motion of particle P. With a known distance of 12 m12m between points A and B, the primary goal of this numerical endeavor is to express, in terms of the particle’s mass (�m), the magnitude of the force acting against the motion of particle P. Through the application of Newtonian principles and kinematics, this exploration delves into the nuanced dynamics of deceleration, offering insights into the resistance forces influencing the particle’s journey.
Douglas Quadling Mechanics1 Exercise 2A Q7
A particle P of mass m kg is moving in a straight line with constant deceleration…………
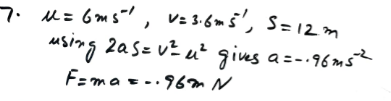
1. Introduction:
A particle P of mass m kg is moving in a straight line with constant deceleration.
- The scenario involves a particle (P) with mass � kgmkg moving along a straight line, experiencing constant deceleration.
2. Scenario Description:
- Particle P traverses from point A to point B, exhibiting speeds of 6 m/s6m/s at A and 3.6 m/s3.6m/s at B.
- The known distance between points A and B is 12 m12m.
3. Objectives:
- The primary goal is to determine, in terms of the particle’s mass (�m), the magnitude of the force resisting the motion of particle P.
4. Significance:
- Understanding the resisting force sheds light on the factors influencing the deceleration of particle P, providing insights into its motion dynamics.
5. Exploration Focus:
- The numerical inquiry centers on the relationship between deceleration, mass, and the resulting force, unraveling the forces at play during the particle’s motion.
6. Newtonian Principles:
- The exploration draws on fundamental principles of Newtonian mechanics, particularly those related to deceleration, to model the motion of particle P.
7. Kinematics:
- The scenario involves complexities related to the kinematics of deceleration, necessitating an analysis of speed changes and resulting forces.
8. Practical Application:
- Findings contribute to the practical understanding of forces influencing particle motion, providing real-world implications for dynamic scenarios involving deceleration.
Conclusion:
A particle P of mass m kg is moving in a straight line with constant deceleration.
- The numerical investigation promises to express, in terms of the particle’s mass (�m), the magnitude of the force resisting the motion of particle P, offering valuable insights into the dynamics of deceleration in particle motion.
