#1 Title: Roadside Rescue: Unveiling Car Acceleration Under Tension: A van is pulling a broken-down car of mass 1200 kg along a straight horizontal road……
Amidst the hum of traffic, a numerical scenario unfolds as a van steps in to rescue a broken-down car stranded on the roadside. The car, with a mass of 1200 kg, finds itself tethered to the van through a horizontal towbar. The sole force influencing the car’s motion is the tension in this towbar, quantified at a robust 750 N. The heart of this scenario lies in calculating the acceleration of the car, a crucial parameter in understanding the dynamics of its rescue journey
Douglas Quadling Mechanics1 Exercise 2A Q2
A van is pulling a broken-down car of mass 1200 kg along a straight horizontal road……..
S
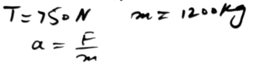
#2 Scope without Calculation: Dynamics of Car Acceleration Under Tension
1. Introduction:
A van is pulling a broken-down car of mass 1200 kg along a straight horizontal road.,,,,
- The scenario involves a van pulling a broken-down car of mass 1200 kg along a straight horizontal road, where the sole force affecting the car’s motion is the tension in the towbar.
2. Scenario Description:
- The focus is on unraveling the acceleration of the car, dictated by the tension in the towbar, as the van endeavors to rescue the stranded vehicle.
3. Objectives:
- The primary goal is to calculate the acceleration of the car, shedding light on the forces at play during its rescue journey.
4. Significance:
- Understanding the car’s acceleration under tension provides insights into the dynamics of towing and the interplay between forces and motion.
5. Exploration Focus:
- The numerical inquiry centers on analyzing the relationship between tension, mass, and acceleration, offering a glimpse into the forces guiding the broken-down car’s rescue.
6. Newtonian Mechanics:
- The exploration draws on fundamental principles of Newtonian mechanics, particularly the force-mass-acceleration relationship, to model the car’s motion.
7. Towing Dynamics:
- The scenario involves complexities related to the dynamics of towing, necessitating an analysis of tension forces and their impact on the car’s acceleration.
8. Practical Application:
- Findings contribute to the practical understanding of forces at play in roadside rescues, providing real-world implications for optimizing towing procedures and vehicle recovery.
Conclusion:
A van is pulling a broken-down car of mass 1200 kg along a straight horizontal road…….
- The numerical investigation promises to unveil the acceleration of the car under tension, offering valuable insights into the dynamic forces shaping the rescue mission on the horizontal road.
