A marathon competitor running at 5 m s1 puts on a sprint when she is 100 metres from the finish, and covers this distance in 16 seconds. Assuming that her acceleration is constant, use the equation s= = (u+v)t to find how fast she is running as she crosses the finishing line.

3 October 2023 by alevelmechanics1.com

Title: Sprint to Glory: Marathoner’s Accelerated Finish

---

Introduction: In the final stretch of a marathon, a competitor, propelled by a surge of determination, ignites a sprint just 100 meters from the finish line. This numerical exploration unveils the dynamics of her accelerated finish, delving into the realm of constant acceleration. By harnessing the equation s = ut + 0.5at², the quest is to discern the speed at which she gracefully crosses the finish line.

Scenario Overview: Imagine the marathoner, a symbol of endurance, injecting a burst of acceleration in the closing moments of the race. The sprint covers a concise yet impactful distance of 100 meters within a time frame of 16 seconds.

Objectives: The primary goal is to ascertain the velocity at the exact moment when the marathoner crosses the finish line. By leveraging the kinematic equation, this exploration captures the essence of her accelerated sprint.

Significance: Understanding the sprint’s acceleration and the resultant velocity adds a layer of significance to the marathoner’s journey. This acceleration burst becomes a testament to the competitor’s strategic prowess, culminating in a triumphant finish.

Accelerated Finish: The numerical exploration unravels the mathematical intricacies of the marathoner’s accelerated sprint. The equation s = ut + 0.5at² becomes the conduit for deciphering the speed that propels her across the finish line.

Mathematical Calculations: The application of the kinematic equation unveils the accelerated sprint’s velocity, a numeric representation of the competitor’s heightened pace during the final 100 meters.

Visualization: While numbers tell a story, a visual representation through graphs or diagrams could illuminate the dynamic shift in the marathoner’s speed during the accelerated sprint, creating a visual crescendo to the narrative.

Douglas Quadling Mechanics 1
Exercise 1B Q2

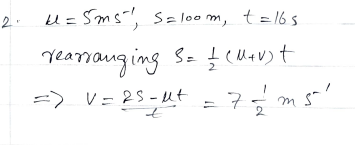
Conclusion:

As the marathoner embraces an accelerated finish, this numerical exploration dissects the mathematical underpinnings of her sprint. The calculated velocity stands as a testament to the surge of acceleration propelling her toward the finish line. In the numeric dance of distance, time, and acceleration, the exploration captures the essence of a strategic burst, infusing the marathoner’s journey with a sprinting crescendo, a finale to the enduring race.

CategoriesChapter 1, Exercise 1B

A police car accelerates from 15 m s to 35 ms in 5 seconds. The acceleration is constant. Illustrate this with a velocity-time graph. Use the equation v=u+ at to calculate the acceleration. Find also the distance travelled by the car in that time.

A train travelling at 20 m s1 starts to accelerate with constant acceleration. It covers the next kilometre in 25 seconds. Use the equation s = ut+at2 to calculate the acceleration. Find also how fast the train is moving at the end of this time. Illustrate the motion of the train with a velocity-time graph. How long does the train take to cover the first half kilometre?

Leave a comment

Logged in as alevelmechanics1.com. Edit your profile. Log out? Required fields are marked *