The Problem:
A boy kicks a football up a slope with a speed of 6 m s1. The ball decelerates at 0.3 m s 2. How far up the slope does it roll?
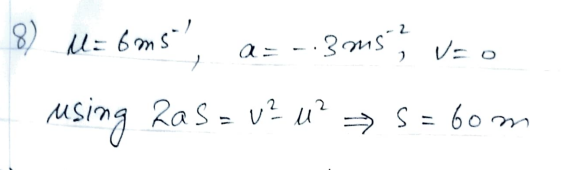
A boy kicks a football up a slope with a speed of 6 m/s. The ball decelerates at 0.3 m/s². How far up the slope does it roll?
Solution:
- Initial speed (u) = 6 m/s
- Deceleration (a) = -0.3 m/s² (negative because it’s slowing down)
- Final speed (v) = 0 m/s (the ball stops at the highest point)
Using the equation of motion:
v² = u² + 2as
Rearranged to solve for distance (s):
s = (v² - u²) / (2a)
Plugging in the values:
s = (0 - 36) / (2 * -0.3)
s = -36 / -0.6
s = 60 meters
Answer: The football rolls 60 meters up the slope before coming to rest.