A freight train 1/4 km long takes 20 seconds to pass a signal. The train is decelerating at a constant rate, and by the time the rear truck has passed the signal it is moving 10 kilometres per hour slower than it was when the front of the train passed the signal. Find the deceleration in kilometre-hour units, and the speed at which the train is moving when the rear truck has just passed the signal.

A freight train, spanning a length of 1/4km, requires 20 seconds to traverse a signal. The train undergoes a constant deceleration, and as the rear truck clears the signal, its speed is
10 kilometers per hour less than it was when the front of the train initially passed the signal. The task at hand involves determining the deceleration of the train in kilometer−hour units, along with the speed of the train as the rear truck completes its passage beyond the signal.

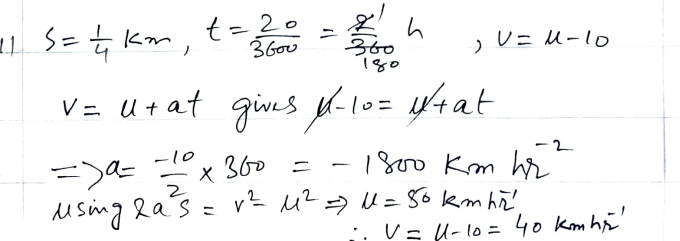
Let’s denote the initial speed of the train as V in kilometers per hour (km/h), and its deceleration as a in kilometers per hour squared (km/h²). The length of the train is given as 1/4 km.When the front of the train passes the signal, the speed is V km/h. When the rear of the train passes the signal, the speed is V−10 km/h.

We can use the equations of motion to relate the distance traveled with time and acceleration. The distance traveled by the rear of the train is the length of the train.