The Problem:
A car travelling at 10 m/s is 25 metres from a pedestrian crossing when the traffic light changes from green to amber. The light remains at amber for 2 seconds before it changes to red. The driver has two choices: to accelerate so as to reach the crossing before the light changes to red, or to try to stop at the light. What is the least acceleration which would be necessary in the first case, and the least deceleration which would be necessary in the second?
Douglas Quadling Mechanics 1
Exercise 1C Q10
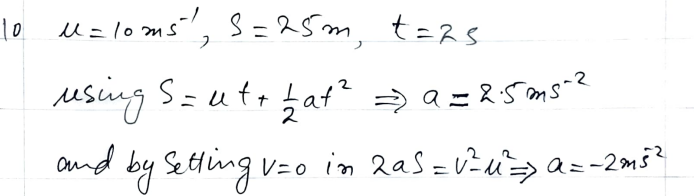
A car traveling at 10 m/s is 25 meters from a pedestrian crossing when the traffic light changes from green to amber. The light remains at amber for 2 seconds before it changes to red. The driver has two choices:
- Accelerate to cross before the light turns red.
- Decelerate to stop before reaching the crossing.
Solution:
Case 1: Accelerating to cross before the light turns red
Using the equation of motion:
s = ut + (1/2) a t²
Rearranged to solve for acceleration (a):
a = 2(s - ut) / t²
Plugging in the values:
a = 2(25 - (10 × 2)) / 2²
a = 2(5) / 4
a = 2.5 m/s²
Result: The car must accelerate at least at 2.5 m/s² to cross the pedestrian crossing before the light turns red.
Case 2: Decelerating to stop before reaching the crossing
Using the equation of motion:
v² = u² + 2as
Rearranged to solve for deceleration (a):
a = -u² / (2s)
Plugging in the values:
a = -(10)² / (2 × 25)
a = -100 / 50
a = -2 m/s²
Result: The car must decelerate at least at 2 m/s² to stop before reaching the pedestrian crossing.
Final Answer:
- Minimum acceleration to cross before the light turns red: 2.5 m/s²
- Minimum deceleration to stop before the crossing: 2 m/s²