Title: Cyclist’s Descent: A Gravity-Powered Journey
Introduction: Embarking on a gravity-powered journey, a cyclist conquers the ascent to the top of a hill, only to release the brakes and free-wheel down the slope. This numerical exploration unravels the dynamics of the cyclist’s descent, encompassing expressions for speed and distance over time, culminating in insights into the duration of the descent and the cyclist’s final velocity.
Scenario Overview: A cyclist, perched at the summit of a hill, initiates a free-wheel descent, propelled by the force of gravity. The hill stretches out over 165 meters, providing the backdrop for an exploration into the intricacies of the cyclist’s descent.
Objective: This exploration aims to formulate expressions representing the cyclist’s speed and the distance covered over a span of time during the descent. Subsequently, it delves into determining the duration of the descent and the cyclist’s final velocity upon reaching the bottom of the hill.
Mathematical Expressions:
- Speed Expression: The cyclist’s speed during the descent is expressed as a function of time, considering the acceleration due to gravity.�(�)=�+��v(t)=u+at
- Distance Expression: The distance covered by the cyclist is articulated as a function of time during the free-wheel descent.�(�)=��+12��2s(t)=ut+21at2
Numerical Analysis: Leveraging the expressions, a numerical analysis unfolds, shedding light on the time it takes for the cyclist to journey from the hill’s summit to its base and the corresponding final velocity attained.
Significance: This exploration delves into the fundamental principles of gravitational acceleration and its influence on the dynamics of a cyclist’s descent. The findings offer valuable insights into the temporal and velocity aspects of free-wheeling down a hill.
Douglas Quadling Mechanics1 Exercise1C Q9
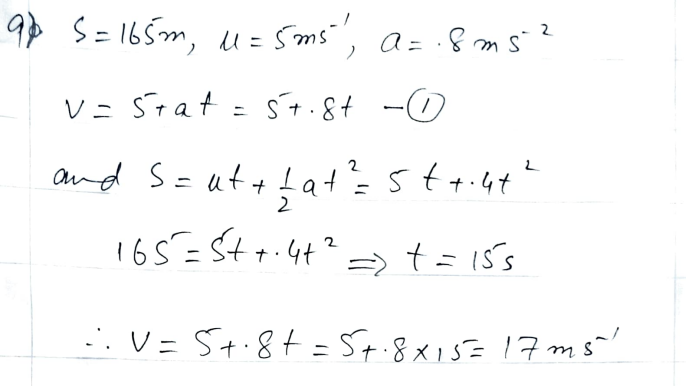
Conclusion:
As the cyclist descends down the 165-meter hill, propelled by gravity, the expressions for speed and distance serve as mathematical guides. The exploration culminates in revelations about the duration of the descent and the cyclist’s velocity upon reaching the hill’s bottom, enriching our understanding of the interplay between physics and cycling dynamics.
