Introduction:
In the given numerical scenario, we are presented with a motorboat of mass 8 tonnes moving along a straight course at a constant speed of 28 km/h. The boat is subjected to a constant forward force with a magnitude of 780 N. The primary objective is to determine the force resisting the motion, assumed to be constant. Subsequently, the scenario explores the situation where the boat’s engine is shut off, and we are tasked with calculating the time it takes for the motorboat to come to a complete stop. It is emphasized that the resistance to motion remains constant throughout this deceleration process. The solution will involve applying principles of Newtonian mechanics to analyze the forces acting on the boat and using relevant kinematic equations to determine the stopping time accurately.
Douglas Quadling Mechanics1 Exercise 2B Q14
Solution:
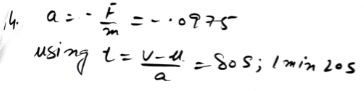
Scope:
The scope of the numerical includes the application of fundamental principles of physics, particularly Newtonian mechanics and kinematics, to analyze the forces acting on the motorboat. The problem involves the interplay of forces, including the propelling force and the resisting force, as well as the impact of the boat’s mass on its motion.
To solve the numerical, the following steps are likely to be involved:
- Application of Newton’s second law to find the net force acting on the boat.
- Determination of the force resisting motion, which is assumed to remain constant.
- Application of relevant kinematic equations to calculate the time it takes for the motorboat to stop after the engine is shut off.
The solution will likely require converting units, applying appropriate formulas, and making accurate calculations. The final answer, representing the time it takes for the motorboat to stop, is expected to be in seconds and rounded to the nearest second.
Overall, the scope of the numerical involves the practical application of physics concepts to understand and quantify the forces influencing the motion of the motorboat and to calculate its deceleration time under specific conditions.
Conclusion:
The given numerical scenario involves a motorboat with a mass of 8 tonnes traveling at a constant speed of 28 km/h. The boat is subjected to a constant forward force of 780 N, and the task is to determine the force resisting motion, assumed to be constant. Additionally, the problem requires calculating the time it takes for the motorboat to come to a complete stop after the engine is shut off, with the assumption that the resistance to motion remains unchanged.
In conclusion, the solution to this numerical would require applying Newton’s second law of motion to determine the net force acting on the motorboat, which includes both the propelling force and the resisting force. Once the force resisting motion is found, the kinematic equations of motion can be employed to calculate the deceleration and subsequently determine the time it takes for the motorboat to stop.
The process involves a combination of mathematical calculations, unit conversions, and the application of physics principles to model and analyze the boat’s motion. The final result, expressed in seconds and rounded to the nearest second, represents the time required for the motorboat to come to rest after the engine is turned off, assuming constant resistance. This numerical problem provides a practical application of physics concepts in understanding and predicting the dynamics of a moving object subject to external forces.
