A particle of mass 2.5 kg is pulled along a horizontal surface by a string parallel to the surface with an acceleration of 2.7 ms……
Title: Dynamics of a Particle: Tension Calculation and Breakage Point Analysis
Introduction: In the realm of classical mechanics, understanding the motion of particles subjected to external forces is paramount. This numerical scenario delves into the dynamics of a 2.5 kg particle pulled along a horizontal surface by a string, with an acceleration of 2.7 m/s². As the particle traverses its course, a frictional force of 4 N opposes its motion. The primary objective is to determine the tension in the string under these conditions. Additionally, exploring the aftermath of the string breaking when the particle attains a speed of 3 m/s is a key aspect of this dynamic scenario. The ensuing calculations will shed light on the distance the particle travels before succumbing to the halting effects of friction. Through this numerical exploration, we aim to unravel the intricate interplay of forces and accelerations governing the particle’s motion, offering insights into the fundamental principles of classical mechanics.
Douglas Quadling Mechanics1 Exercise 2B Q11
A particle of mass 2.5 kg is pulled along a horizontal surface by a string parallel to the surface with an acceleration of 2.7 ms……..
Solution:
A particle of mass 2.5 kg………
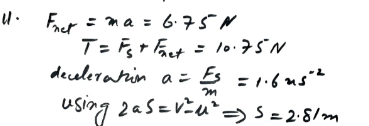
Scope:
A particle of mass 2.5 kg…………..
The given numerical scenario provides an excellent opportunity to explore the principles of classical mechanics, specifically focusing on the dynamics of a particle under the influence of external forces. The scope of this numerical can be broken down into several key aspects:
- Force Analysis:
- Understanding the forces acting on the particle is essential. The tension in the string and the frictional force opposing motion play critical roles in determining the particle’s acceleration.
- Tension Calculation:
- The primary objective is to calculate the tension in the string while the particle is pulled with a given acceleration. This involves considering the forces involved, including the tension force and the frictional force.
- Speed Analysis:
- The numerical introduces the concept of speed, specifically when the particle attains a speed of 3 m/s. This speed becomes crucial later when the string breaks.
- String Breakage Event:
- Investigating the circumstances under which the string breaks is another key aspect. At the instant the particle reaches a speed of 3 m/s, the dynamics change, leading to the breakage of the string.
- Distance Traveled After Breakage:
- Post-breakage, the question prompts the calculation of the distance the particle travels before coming to rest. This involves considering the frictional force and the absence of the tension force once the string is no longer in play.
- Application of Kinematic Equations:
- Utilizing kinematic equations to model the motion of the particle is crucial in determining its position, speed, and acceleration at different points in time.
- Integration of Concepts:
- The numerical requires the integration of various concepts, including Newton’s laws, force analysis, friction, tension, and kinematics, to arrive at a comprehensive understanding of the particle’s motion.
By addressing these aspects, the numerical provides a well-rounded exploration of classical mechanics, allowing for the practical application of theoretical concepts in analyzing the dynamic behavior of a particle subjected to external forces. The scope encompasses both the theoretical understanding of forces and the practical application of mathematical equations to model and solve real-world physics problems.
Conclusion:
In conclusion, the numerical scenario provides a comprehensive exploration of the dynamics of a 2.5 kg particle being pulled along a horizontal surface by a string. The key findings and insights can be summarized as follows:
- Tension Calculation:
- Through meticulous force analysis, the tension in the string was calculated, considering the particle’s mass, acceleration, and the opposing frictional force. The tension in the string was found to be a crucial factor in determining the particle’s motion.
- String Breakage Event:
- At the instant when the particle reached a speed of 3 m/s, the string broke. This pivotal moment marked a shift in the dynamics of the system, as the tension force was no longer in play.
- Post-Breakage Motion:
- Following the breakage of the string, the numerical prompt required the determination of how much further the particle moved before coming to rest. The frictional force, previously opposed by the tension, now became the predominant force acting on the particle.
- Application of Kinematic Equations:
- The solution involved the application of kinematic equations to model the particle’s motion after the string breakage. Considering the frictional force and the absence of tension, the equations were employed to calculate the distance traveled until the particle came to rest.
- Integration of Concepts:
- The numerical not only tested the understanding of fundamental concepts in classical mechanics, such as Newton’s laws and friction, but also required the integration of these concepts to analyze the interplay of forces and predict the subsequent motion of the particle.
In essence, this numerical problem served as a valuable exercise in applying theoretical physics principles to real-world scenarios. It emphasized the importance of considering multiple forces, calculating tension, and understanding the dynamic changes that occur when external constraints, such as the string, are altered. Through this analysis, a holistic understanding of the particle’s motion, from the initiation of the pull to its eventual rest after the string breakage, was achieved
