A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s………………..
Title: Braking Dynamics: Determining Force on a Railway Engine
Introduction:
A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s………………
In the realm of mechanical dynamics, the interaction between a moving object and an opposing force, such as brakes or buffers, plays a crucial role in understanding the system’s behavior. This numerical scenario focuses on a railway engine with a mass of 5000 kg that is initially moving at a velocity of 0.25 m/s. The narrative takes a dramatic turn when the engine encounters buffers in a siding, leading to its rapid deceleration and eventual rest within a span of 0.4 seconds. The central objective of this numerical challenge is to unravel the force exerted on the engine by the buffers during this abrupt deceleration. By delving into the principles of kinetic motion, Newton’s laws, and the dynamics of forces, this scenario provides an opportunity to quantify the force applied to bring the moving engine to a sudden stop.
Douglas Quadling Mechanics1 Exercise 2B Q9
A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s…………………….
Solution:
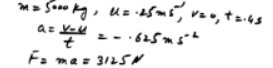
Scope:
A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s……………..
The numerical scenario involving the railway engine presents a multifaceted scope that involves various aspects of classical mechanics and dynamics. The key elements and scope of this numerical can be outlined as follows:
- Kinematics and Initial Conditions:
- Analyzing the initial conditions of the railway engine, including its mass and initial velocity, forms the basis for understanding the system’s kinetic energy.
- Deceleration and Braking:
- The abrupt deceleration of the engine upon striking the buffers signifies the application of a braking force. Investigating the factors influencing this deceleration is central to the numerical’s scope.
- Time of Braking:
- The specified time of 0.4 seconds within which the engine comes to rest provides a temporal constraint. Understanding the time frame of the deceleration contributes to determining the magnitude of the force applied.
- Application of Newton’s Second Law:
- Newton’s second law, relating force, mass, and acceleration, serves as a fundamental principle for analyzing the dynamics of the railway engine. The numerical involves the application of this law to calculate the force exerted by the buffers during the braking process.
- Force Magnitude Determination:
- The primary objective is to calculate the magnitude of the force exerted on the engine by the buffers. This involves integrating the concepts of acceleration, mass, and time within the context of deceleration.
- Assumption of Constant Force:
- The numerical assumes that the force exerted by the buffers is constant during the braking process. This assumption simplifies the analysis and allows for the application of equations of motion.
- Practical Implications:
- Beyond the numerical calculations, the scenario provides insights into the practical considerations of braking systems in railway engineering. Understanding the forces involved is essential for designing effective braking mechanisms.
- Concepts of Energy and Work:
- The conversion of kinetic energy to work done by the braking force is inherent in the scenario. This introduces additional concepts related to energy transfer and work during the deceleration process.
By addressing these aspects, the numerical not only tests the understanding of fundamental principles in classical mechanics but also provides a practical context for analyzing the forces involved in bringing a moving object to rest, contributing to a broader understanding of dynamics in real-world scenarios.
Conclusion:
A railway engine of mass 5000 kg is moving at 0.25 ms when it strikes the buffers in a siding. Given that the engine is brought to rest in 0.4 s………..
In conclusion, the numerical scenario featuring the railway engine presented a comprehensive exploration of the dynamics involved in the abrupt deceleration of a moving object. Key findings and insights from the analysis can be summarized as follows:
- Initial Conditions and Kinematics:
- The scenario commenced with an understanding of the initial conditions, including the mass of the railway engine and its initial velocity. This laid the groundwork for the subsequent analysis of kinetic energy and motion.
- Deceleration and Braking Force:
- The sudden deceleration of the engine upon striking the buffers indicated the application of a braking force. The objective of the numerical challenge was to quantify this force exerted by the buffers during the deceleration process.
- Time Constraint:
- The specified time of 0.4 seconds during which the engine comes to rest provided a temporal constraint for the analysis. Considering this time frame was crucial in determining the magnitude of the braking force.
- Application of Newton’s Second Law:
- Newton’s second law was employed to relate the force, mass, and acceleration of the railway engine during the braking process. This fundamental principle allowed for the calculation of the force exerted by the buffers.
- Constant Force Assumption:
- The numerical assumed that the force exerted by the buffers was constant during the braking period. This simplification facilitated the application of equations of motion, providing a practical approach to the analysis.
- Force Magnitude Determination:
- The primary objective was successfully achieved by calculating the magnitude of the force exerted by the buffers on the railway engine. This numerical solution encapsulated the dynamic interplay of forces leading to the engine’s rapid deceleration.
- Practical Considerations:
- Beyond the numerical calculations, the scenario offered insights into the practical considerations of braking systems in railway engineering. The analysis of forces contributes to the understanding of the engineering principles involved in designing effective braking mechanisms.
In essence, this numerical problem provided a valuable exercise in applying fundamental principles of classical mechanics to real-world scenarios. It underscored the significance of understanding the forces involved in bringing a moving object to rest, offering a glimpse into the intricacies of dynamic systems and the practical considerations of railway engineering
