Title: Driving Dynamics: Analyzing Forces in Car Motion A car of mass 1200 kg is moving with a constant speed of 20 m s in a horizontal straight line, against a resisting force of 300 N………
Introduction:
A car of mass 1200 kg is moving with a constant speed of 20 m s in a horizontal straight line, against a resisting force of 300 N…….
The motion of a car involves a delicate equilibrium between driving forces and resisting forces, providing a captivating scenario for physics analysis. In this numerical challenge, a car with a mass of 1200 kg maintains a constant speed of 20 m/s against a resisting force of 300 N. The initial question pertains to determining the driving force required to sustain this constant motion. The scenario evolves as the driver opts for acceleration, uniformly increasing the speed to 30 m/s over a 30-second interval, all while the resisting force remains a constant 300 N. The central focus of this numerical exploration is to calculate the additional driving force generated during this acceleration phase, offering insights into the dynamic interplay of forces governing the car’s motion.
Solution:
A car of mass 1200 kg is moving with a constant speed of 20 m s in a horizontal straight line, against a resisting force of 300 N……
Douglas Quadling Mechanics1 Exercise 2B Q4
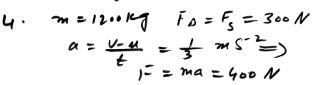
Scope:
A car of mass 1200 kg is moving with a constant speed of 20 m s in a horizontal straight line, against a resisting force of 300 N…….
- Initial Motion (constant speed):
- The car is moving with a constant speed of 20 m/s20m/s.
- Against a resisting force of 300 N.
- The driving force required to sustain this constant speed is equal to the resisting force (300 N).
- Acceleration Phase (speeding up uniformly):
- The driver accelerates the car uniformly to reach a new speed of 30 m/s30m/s over a time period of 30 s.
- The resisting force remains constant at 300 N
- During this acceleration phase, there is an additional driving force needed to overcome the resisting force and accelerate the car.
So, the problem involves determining the driving force required to maintain the initial constant speed (equal to the resisting force) and calculating the extra driving force needed during the acceleration phase to reach the new speed of 30 m/s
Conclusion:
In this scenario, the car initially moves at a constant speed of 20 m/s against a resisting force of 300 N. The driving force required to maintain this constant speed is equal to the resisting force. Subsequently, the driver accelerates the car uniformly, reaching a new speed of 30 m/s over a 30 s time span. Despite the constant resisting force of 300 N, an additional driving force is needed during the acceleration phase to overcome resistance and achieve the higher speed. This extra driving force is determined through the application of Newton’s second law, emphasizing the dynamic interplay between forces, mass, and acceleration. The calculation of the extra driving force offers insights into the energy requirements for the car’s acceleration and underscores the intricate balance of forces involved in the motion of the vehicle.
