Introduction:A boy is pushing one side of a box, of mass m kg, with a force of 25 N. His sister is pushing from the opposite side of the box with a force of 13 N…..
In the realm of classical mechanics, a scenario unfolds as a boy and his sister exert opposing forces on a stationary box. The boy applies a force of 25 N in one direction, while the sister counters with 13 N in the opposite direction. Despite this apparent equilibrium, the box remains immobile, held in check by a frictional force resisting motion with a magnitude of 3mN, where m is the mass of the box in kilograms. This numerical conundrum prompts an investigation into the mass of the box, with the ultimate goal of determining the value of m. Furthermore, a dynamic twist unfolds as the boy amplifies his efforts, now exerting a force of 35 N. The ensuing challenge involves showcasing that, with the frictional force persisting, the box undergoes acceleration at a rate of 2.5 m/s2. This exploration navigates the delicate equilibrium of forces and accelerative dynamics, encapsulating a captivating interplay of mass, friction, and applied forces.
Douglas Quadling Mechanics1 Exercise 2B Q2
A boy is pushing one side of a box, of mass m kg, with a force of 25 N. His sister is pushing from the opposite side of the box with a force of 13 N…….
Solution:
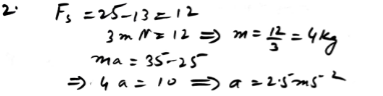
Scope
A boy is pushing one side of a box, of mass m kg, with a force of 25 N. His sister is pushing from the opposite side of the box with a force of 13 N……..
In the fascinating realm of mechanics, this numerical scenario unveils the delicate equilibrium of forces acting on a stationary box. A boy exerts a force of 25 N in one direction, while his sister counters with 13 N in the opposite. The box resists motion, maintaining stillness against the nuanced interplay of forces. The challenge presented is to determine the mass (m) of the box, given the equilibrium and the known magnitude (3mN) of the frictional force impeding motion.
Adding complexity to the narrative, the boy amplifies his efforts to 35 N, introducing a dynamic dimension. The subsequent exploration involves showcasing that, with the frictional force persisting, the box undergoes acceleration at a rate of 2.5 m/s2. This numerical journey unfolds the mysteries of equilibrium, friction, and acceleration, offering a comprehensive understanding of the intricate forces shaping the box’s motion.
Conclusion
A boy is pushing one side of a box, of mass m kg, with a force of 25 N. His sister is pushing from the opposite side of the box with a force of 13 N……….
In the captivating dynamics of this numerical scenario, the equilibrium of forces on a stationary box reveals an intricate interplay. The boy exerts a force of 25 N, while his sister counters with 13 N, creating a delicate balance. The immobility of the box, defying the applied forces, becomes a puzzle unraveled by the introduction of a frictional force with a magnitude of 3mN, where m represents the mass of the box. The resolution of this equilibrium conundrum leads to the determination of the mass (m).
Adding a dynamic dimension, the boy enhances his force to 35 N, setting the stage for acceleration. The conclusion showcases the acceleration of the box at 2.5 m/s2 while the frictional force persists, emphasizing the nuanced dynamics of forces and acceleration within the realm of classical mechanics. This exploration illuminates the intricate physics governing the motion of the box, offering a comprehensive understanding of its equilibrium and subsequent dynamic response.
