A wooden block of mass m kg is at rest on a table, 1.6 metres from an edge. The block is pulled directly towards the edge by a horizontal string………..
Introduction:
In classical mechanics, the study of motion involves understanding the forces acting on an object and how these forces influence its movement. One of the fundamental principles in this domain is Newton’s second law of motion, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This principle is pivotal in solving various real-world problems, such as determining the motion of objects under the influence of forces. In this context, we will analyze a problem involving a wooden block being pulled across a table by a horizontal string. The goal is to calculate the time taken for the block to reach the edge of the table under the influence of a given tension in the string
Solution
A wooden block of mass m kg is at rest on a table, 1.6 metres from an edge. The block is pulled directly towards the edge by a horizontal string………..
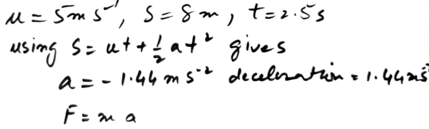
Scope
A wooden block of mass m kg is at rest on a table, 1.6 metres from an edge. The block is pulled directly towards the edge by a horizontal string……
The scope of this problem includes the following aspects:
- Understanding the Forces Involved: We will identify the forces acting on the wooden block, including the tension in the string and any opposing forces such as friction, though the latter is assumed to be negligible in this problem.
- Applying Newton’s Second Law: Using Newton’s second law, we will establish the relationship between the force exerted by the string, the mass of the block, and its acceleration.
- Kinematic Equations: We will use the kinematic equations of motion to calculate the time taken for the block to travel a specified distance (1.6 meters in this case) given its acceleration.
- Assumptions and Simplifications: Assumptions such as the neglect of friction and air resistance will be made to simplify the calculations. These assumptions are reasonable given the context and typical introductory physics problems.
Analysis and Calculations
A wooden block of mass m kg is at rest on a table, 1.6 metres from an edge. The block is pulled directly towards the edge by a horizontal string…….
Step 1: Identifying the Forces
The block is subjected to a horizontal force due to the tension TTT in the string. Given that the tension is 0.2m0.2m0.2m N, where mmm is the mass of the block in kilograms, we can write:
T=0.2m NT = 0.2m \, \text{N}T=0.2mN
Since the block is initially at rest, and we assume no friction or other horizontal forces acting on it, the net force FFF on the block is equal to the tension:
F=T=0.2m NF = T = 0.2m \, \text{N}F=T=0.2mN
Step 2: Applying Newton’s Second Law
According to Newton’s second law:
F=maF = maF=ma
where aaa is the acceleration of the block. Substituting the expression for the force, we get:
0.2m=ma0.2m = ma0.2m=ma
Dividing both sides by mmm:
a=0.2 m/s2a = 0.2 \, \text{m/s}^2a=0.2m/s2
Thus, the acceleration of the block is 0.2 m/s20.2 \, \text{m/s}^20.2m/s2.
Step 3: Using Kinematic Equations
We need to find the time ttt it takes for the block to travel a distance d=1.6d = 1.6d=1.6 meters from rest under constant acceleration. The kinematic equation that relates distance ddd, initial velocity v0v_0v0, acceleration aaa, and time ttt is:
d=v0t+12at2d = v_0 t + \frac{1}{2}at^2d=v0t+21at2
Since the initial velocity v0=0v_0 = 0v0=0 (the block starts from rest), the equation simplifies to:
d=12at2d = \frac{1}{2}at^2d=21at2
Substituting the known values (d=1.6d = 1.6d=1.6 m and a=0.2 m/s2a = 0.2 \, \text{m/s}^2a=0.2m/s2):
1.6=12(0.2)t21.6 = \frac{1}{2}(0.2)t^21.6=21(0.2)t2
1.6=0.1t21.6 = 0.1t^21.6=0.1t2
Dividing both sides by 0.1:
t2=16t^2 = 16t2=16
Taking the square root of both sides:
t=4 secondst = 4 \, \text{seconds}t=4seconds
Conclusion
A wooden block of mass m kg is at rest on a table, 1.6 metres from an edge. The block is pulled directly towards the edge by a horizontal string……
The time taken for the wooden block to reach the edge of the table, given a tension of 0.2m0.2m0.2m N in the horizontal string and assuming negligible friction, is 4 seconds. This problem illustrates the application of Newton’s second law and kinematic equations in determining the motion of an object under constant acceleration. By breaking down the forces acting on the block and using fundamental principles of mechanics, we derived a straightforward solution that can be applied to similar problems in classical mechanics.
