Title: Analyzing Cyclist’s Journey: (t,v) Graph Dynamics: The figure shows the (t,v) graph for the motion of a cyclist; the graph consists of three straight line segments……
Scope: Unveiling Acceleration and Total Distance in Cyclist’s Motion
1. Introduction:The figure shows the (t,v) graph for the motion of a cyclist; the graph consists of three straight line segments….
- The journey of a cyclist unfolds through the lens of a (t,v) graph, characterized by three distinct straight line segments. This exploration delves into the dynamics encapsulated by the graph, aiming to decipher the acceleration of the cyclist at a specific moment and determine the total distance covered during the recorded time interval.
2. Scenario Description:
- The graph intricately captures the cyclist’s motion, featuring three straight line segments. This exploration seeks to leverage the graph’s information to pinpoint the cyclist’s acceleration precisely when t equals 2 seconds. Additionally, the total distance traveled by the cyclist for the recorded time interval becomes a focal point of analysis.
3. Objectives:
- The primary objectives include determining the cyclist’s acceleration at t=2 seconds and calculating the total distance covered within the recorded time interval based on the provided (t,v) graph.
4. Significance:
- The significance lies in unraveling the intricate dynamics of a cyclist’s motion, as depicted by the (t,v) graph. Insights gained contribute to understanding the interplay between time, velocity, and acceleration in the cyclist’s journey.
5. Exploration Focus:
- The exploration centers on deciphering the nuances of acceleration at a specific moment and calculating the total distance traveled, leveraging the visual representation provided by the (t,v) graph.
6. Dynamics of the Graph:
- Core dynamics involve analyzing the slopes and characteristics of the three straight line segments on the graph, enabling the extraction of crucial information related to acceleration and distance.
7. Acceleration at t=2:
- Analysis includes determining the precise acceleration of the cyclist when the time variable t equals 2 seconds. The graph’s slope and characteristics contribute to this insightful calculation.
8. Total Distance Calculation:
- The exploration incorporates mathematical calculations based on the graph’s information to ascertain the total distance covered by the cyclist within the recorded time interval, showcasing the practical application of graph analysis in motion dynamics.
Douglas Quadling Mechanics1 Miscellaneous Exercise1 Q5
The figure shows the (t,v) graph for the motion of a cyclist; the graph consists of three straight line segments…….
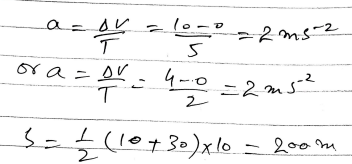
Graphical Interpretation:
- The graphical representation of the (t,v) graph serves as a visual aid in interpreting the cyclist’s journey, enabling a deeper understanding of the acceleration and distance dynamics.
Conclusion:
The figure shows the (t,v) graph for the motion of a cyclist; the graph consists of three straight line segments…….
- The exploration promises to unveil the acceleration at a specific moment and calculate the total distance covered by the cyclist, offering a comprehensive view of the motion dynamics encapsulated by the (t,v) graph in the cyclist’s journey.
The Next Question: https://alevelmechanics1.com/602/a-car-is-waiting-at-traffic-lights-with-a-van-behind/
