Title: Braking Ballet: Deceleration Dynamics of a Stopping Car:A car comes to a stop from a speed of 30 m s in a distance of 804 m. The driver brakes so as to produce a deceleration of m s2 to begin with…
Introduction:
A car comes to a stop from a speed of 30 m s in a distance of 804 m. The driver brakes so as to produce a deceleration of m s2 to begin with…
In a dramatic symphony of deceleration, a car hurtles towards a stop from an initial velocity of 30 m/s. The driver orchestrates a braking performance, initiating with a gentle deceleration “a” and intensifying the maneuver with a more pronounced deceleration “b.” This numerical exploration delves into the intricate dance of deceleration, unveiling the speed of the car at the moment of heightened braking and calculating the total temporal spectacle of its dramatic stop.
Scenario Overview: The narrative unfolds on a road where the car, propelled by its initial velocity, undergoes a strategic deceleration orchestrated by the driver.
Objectives:
- Dynamic Deceleration Display (a): Determine the speed of the car precisely at the instant when the driver switches from the initial deceleration “a” to the intensified deceleration “b.”
- Temporal Termination (b): Calculate the total time the car takes to gracefully come to a complete stop, showcasing the temporal dynamics of the deceleration ballet.
Significance: This exploration is significant in unraveling the nuanced dynamics of deceleration, depicting the transition from a moderate to an intensified braking regime.
Exploration Focus: The primary focus lies in dissecting the deceleration dynamics, pinpointing the instant of increased braking intensity, and unraveling the temporal intricacies of the car’s journey to a standstill.
Dynamics of Deceleration: The exploration navigates through the intricacies of deceleration, capturing the evolving speed of the car during the braking ballet.
Mathematical Calculations: Equations of motion, velocity-deceleration relationships, and distance calculations guide the mathematical expressions shaping the exploration.
Visualization: Graphical representations may be utilized to visualize the evolution of speed during the distinct phases of deceleration, enhancing the narrative.
Douglas Quadling Mechanics1 Exercise1D Q5
A car comes to a stop from a speed of 30 m s in a distance of 804 m. The driver brakes so as to produce a deceleration of m s2 to begin with……
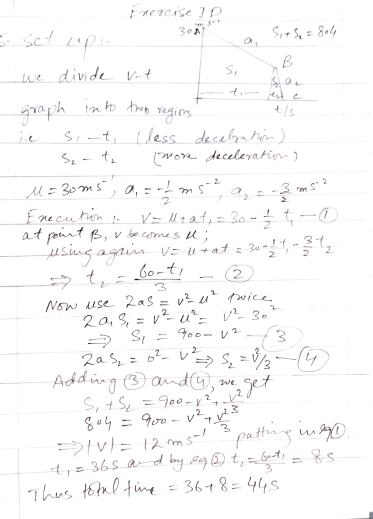
Conclusion:
A car comes to a stop from a speed of 30 m s in a distance of 804 m. The driver brakes so as to produce a deceleration of m s2 to begin with…..
As the numerical journey unfolds, this exploration promises to illuminate the dynamic interplay between varying decelerations, revealing the speed at the moment of intensified braking and unraveling the temporal spectacle of the car’s graceful stop. The quest captures the essence of a braking ballet, portraying the intricacies of deceleration dynamics and the orchestrated performance of a car coming to rest.
The Next Question: https://alevelmechanics1.com/577/a-motorbike-and-a-car-are-waiting-side-by-side-at-traffic-lights/
