Title: Dynamic Journey: Braking at the Junction: A car rounds a bend at 10 ms^-1, and then accelerates at 1/2ms^-2 along a straight stretch of road. There is a junction 400 m from the bend…..
Introduction:
A car rounds a bend at 10 ms^-1, and then accelerates at 1/2ms^-2 along a straight stretch of road. There is a junction 400 m from the bend…..
Embarking on a dynamic journey, a car navigates a bend at 10 m/s, accelerates on a straight stretch at 1/2 m/s², and faces a critical decision at a junction 400 m away. The driver, in a choreographed maneuver, applies the brakes, inducing a controlled deceleration to gracefully bring the car to a rest at the junction. This numerical exploration delves into the intricate dance of acceleration, braking, and deceleration, painting a vivid picture of the car’s journey to the junction.
Scenario Overview: The narrative unfolds on a winding road, capturing the car’s motion around a bend, acceleration on a straight stretch, and the pivotal braking phase leading to a halt at the junction.
Objectives:
- Dynamic Graphical Depiction (a): Illustrate the (t, v) graph, portraying the evolving velocity of the car during the entire journey.
- Critical Braking Speed (b): Determine the speed of the car precisely when the driver applies the brakes, capturing the moment of decision at 100 m from the junction.
- Deceleration Dynamics (c): Calculate the deceleration required for the car to come to a rest at the junction, orchestrating a graceful conclusion to its dynamic journey.
Significance: This exploration is significant in unraveling the nuanced dynamics of acceleration, braking, and deceleration, shaping the car’s journey around the bend and leading to a controlled stop at the junction.
Exploration Focus: The primary focus lies in graphically representing the car’s velocity-time profile, pinpointing the critical braking speed, and deciphering the deceleration dynamics.
Dynamic Motion Dynamics: The exploration navigates through the intricacies of acceleration, controlled braking, and the nuanced transition from movement to rest.
Mathematical Calculations: Equations of motion, velocity-time relationships, and distance calculations guide the mathematical expressions shaping the graphical and numerical representations.
Visualization: Graphical representations enhance the narrative, offering a visual depiction of the car’s dynamic journey and the critical braking phase.
Douglas Quadling Mechanics1 Exercise1D Q4
A car rounds a bend at 10 ms^-1, and then accelerates at 1/2ms^-2 along a straight stretch of road. There is a junction 400 m from the bend……..
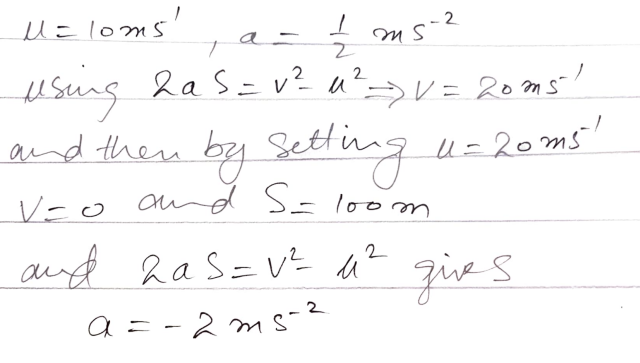
Conclusion:
A car rounds a bend at 10 ms^-1, and then accelerates at 1/2ms^-2 along a straight stretch of road. There is a junction 400 m from the bend……
As the numerical journey unfolds, this exploration promises to capture the essence of a dynamic ride, showcasing the interplay between acceleration, controlled braking, and the precision of deceleration. The quest provides a cinematic glimpse into the car’s journey around the bend, acceleration on the straight stretch, and the strategic braking that culminates in a graceful stop at the junction.
The Next Question: https://alevelmechanics1.com/574/a-car-comes-to-a-stop-from-a-speed-of-30/
