3 October 2023 by alevelmechanics1.com
Title: Soaring to Take-Off: Aircraft Acceleration Odyssey
Introduction: Embarking on the thrilling journey of take-off, this numerical exploration unveils the acceleration escapade of an aircraft. Starting from a standstill, the aircraft accelerates relentlessly, aiming to attain the coveted take-off speed of 60 m/s. The focus lies on deciphering the temporal dynamics of the take-off run and quantifying the aircraft’s acceleration during this exhilarating journey.
Scenario Overview: Picture an aircraft nestled on the runway, its engines roaring to life. The take-off saga begins as the aircraft accelerates, leaving behind a trail of dynamic motion. The runway, a canvas for acceleration, spans 900 meters, providing the stage for the aircraft’s acceleration prowess.
Objective: The primary objective is to unravel the temporal intricacies of the take-off run—determining how long the aircraft requires to reach the take-off speed of 60 m/s. Subsequently, the calculated time is employed to unveil the acceleration experienced by the aircraft during this accelerated ascent.
Significance: Understanding the duration and acceleration of the take-off run is crucial in aviation dynamics. It offers insights into the aircraft’s performance during a critical phase, shedding light on the interplay between distance, time, and acceleration.
Acceleration Odyssey: The acceleration saga unfolds as the aircraft progresses from rest to the exhilarating take-off speed. The constant acceleration transforms the runway into a launchpad, and the calculated time encapsulates the duration of this acceleration odyssey.
Mathematical Calculations: Leveraging kinematic equations, the time required for the aircraft to attain the take-off speed is unveiled. The subsequent calculation divulges the acceleration experienced by the aircraft, a numerical manifestation of its prowess in achieving flight.
Visualization: Graphical representations may visually capture the accelerating dynamics, offering a tangible portrayal of the aircraft’s journey from rest to take-off speed.
Douglas Quadling Mechanics 1
Exercise 1B Q5
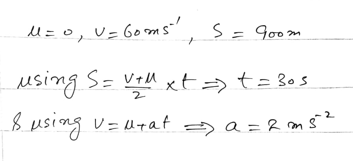
Conclusion:
As the aircraft surges from inertia to the thrill of take-off, this numerical exploration unravels the temporal nuances of the take-off run. The calculated time encapsulates the duration of acceleration, and the derived acceleration value showcases the aircraft’s prowess in navigating the runway’s acceleration canvas. The take-off odyssey, a symphony of motion, finds numerical expression in the interplay of distance, time, and acceleration.
CategoriesChapter 1, Exercise 1B
Leave a comment
Logged in as alevelmechanics1.com. Edit your profile. Log out? Required fields are marked *
