3 October 2023 by alevelmechanics1.com
Title: Pursuit in Motion: Police Car Acceleration Analysis
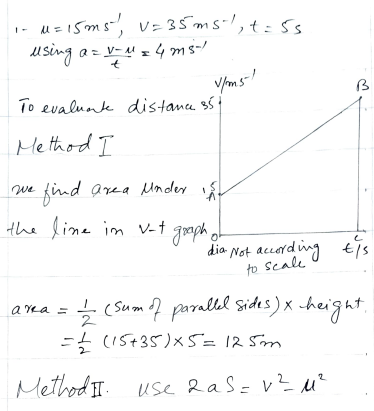
Introduction: In the realm of law enforcement, a police car embarks on a rapid acceleration, surging from 15 m/s to 35 m/s in a mere 5 seconds. This numerical exploration unravels the dynamics of the police car’s acceleration through the lens of a velocity-time graph and employs the kinematic equation v = u + at to unveil the acceleration magnitude. Additionally, the quest extends to quantify the distance traversed by the accelerating police car during this swift interval.
Scenario Overview: Picture a police car navigating the urban landscape, responding to the call of duty. In the span of 5 seconds, the velocity undergoes a seamless transition from 15 m/s to 35 m/s, embodying a scenario where acceleration plays a pivotal role.
Objectives: The primary goals of this exploration are twofold. Firstly, to visually depict the acceleration journey through a velocity-time graph, and secondly, to calculate the acceleration magnitude and the corresponding distance covered using the kinematic equation.
Significance: Understanding the acceleration dynamics of a police car holds significance not only in the context of law enforcement but also in the broader realm of physics. This exploration sheds light on the intricate relationship between velocity, time, and acceleration.
Acceleration Analysis: A graphical representation, in the form of a velocity-time graph, serves as a canvas for illustrating the police car’s acceleration journey. Additionally, the application of the kinematic equation unravels the numerical identity of the acceleration.
Mathematical Calculations: The kinematic equation v = u + at becomes the mathematical beacon guiding the determination of acceleration. Further, it aids in quantifying the distance traveled by the police car during this dynamic acceleration phase.
Visualization: Accompanying the numerical revelations, a visual representation in the form of a velocity-time graph provides an intuitive grasp of the police car’s acceleration trajectory, offering a dynamic snapshot of its changing velocity over time.
Douglas Quadling Mechanics 1
Exercise 1B Q1
Conclusion:
As the police car accelerates with purpose, this numerical exploration encapsulates the essence of its velocity transformation. The velocity-time graph and mathematical calculations intertwine to unveil the acceleration magnitude and the distance covered, enriching the understanding of dynamic motion in the context of law enforcement scenarios.
CategoriesChapter 1, Exercise 1B
The speed limit on a motorway is 120 km per hour. What is this in SI units?
Leave a comment
Logged in as alevelmechanics1.com. Edit your profile. Log out? Required fields are marked *
