Title: Downhill Descent: The Braking Skier’s Journey
Introduction: Embarking on a thrilling downhill descent, a skier accelerates across the finishing line with a speed of 30 m/s. However, the journey doesn’t end there; an immediate deceleration ensues, dictated by the skier’s effort to safely navigate the terrain. This numerical exploration unveils the dynamics of the skier’s deceleration, providing expressions for speed, uncovering details of the skier’s motion, and culminating in a graphical representation.
Scenario Overview: The downhill skier, having crossed the finishing line with zest, engages in a controlled deceleration to navigate the downhill terrain. The journey unfolds with precision, considering the skier’s speed, distance covered, and the eventual halt beyond the finishing line.
Objectives:
- Formulate an expression representing the skier’s speed as a function of the distance beyond the finishing line.
- Calculate the skier’s speed when positioned at specific distances beyond the finishing line.
- Determine the distance the skier falls short of the barrier where she comes to a stop.
- Illustrate the skier’s motion through an (s, v) graph.
Mathematical Expressions:
- Speed Expression: The skier’s speed during deceleration is articulated as a function of the distance beyond the finishing line.�(�)=�−�⋅�v(s)=u−a⋅s
Numerical Analysis: Leveraging the speed expression, a numerical analysis unfolds, providing insights into the skier’s speed at designated distances and the shortfall from the barrier where the skier eventually halts.
Graphical Representation: An (s, v) graph visually captures the skier’s motion, portraying the correlation between distance covered and speed during the controlled deceleration.
Douglas Quadling Mechanics1 Exercise1C Q7
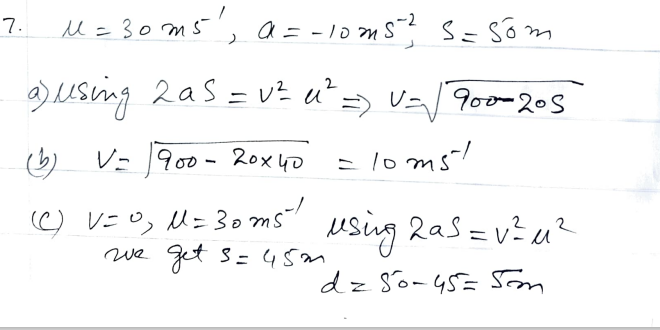
Conclusion:
As the downhill skier gracefully maneuvers the post-finishing line descent, the expressions and graphical representation become valuable tools. The exploration offers a nuanced understanding of the skier’s deceleration dynamics, revealing crucial details about speed, distance, and the precise point where the skier halts. This numerical journey encapsulates the thrill and precision of downhill skiing, marrying physics with the artistry of controlled motion.
