Title: Acceleration Unveiled: Motor-Scooter Odyssey
Introduction: Embarking on a journey from a state of rest, a motor-scooter gradually unfolds its accelerating prowess, attaining a velocity that intricately corresponds to the distance covered. This numerical exploration seeks to unveil the relationship between speed and distance for a motor-scooter accelerating at a consistent rate.
Scenario Overview: Imagine the hum of a motor-scooter as it navigates through an accelerating journey, beginning from a standstill and progressively gaining speed. This scenario encapsulates the essence of the motor-scooter’s acceleration, quantified by the relationship between its speed (�v) and the distance (�s) covered.
Objectives:
- Establish an expression representing the speed (�v) of the motor-scooter in terms of the distance (�s) covered.
- Illustrate the relationship between speed and distance through a graphical representation, depicting the (s, v) graph.
Mathematical Expression:
- Velocity-Distance Relationship: The speed (�v) of the motor-scooter can be expressed using the kinematic equation:�2=�2+2��v2=u2+2asWhere: �v = final velocity, �u = initial velocity (0 m/s since the motor-scooter starts from rest), �a = acceleration (0.1 m/s²), �s = distance.Simplifying the equation, we get: �=2��v=2as
Graphical Representation: A graphical depiction of the (s, v) relationship showcases the evolving speed of the motor-scooter concerning the distance covered. The graph serves as a visual narrative, capturing the essence of the accelerating journey.
Douglas Quadling Mechanics1 Exercise1C Q3
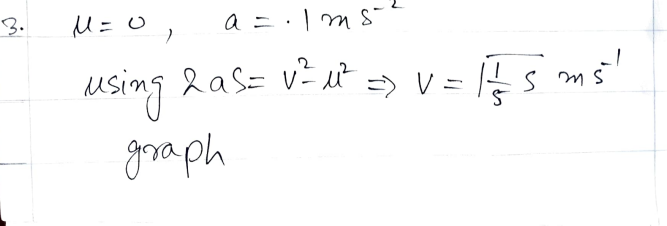
Conclusion:
In the realm of motion dynamics, understanding the nuanced relationship between speed and distance provides valuable insights into the behavior of an accelerating motor-scooter. This exploration not only unveils the mathematical expression governing this relationship but also visually represents it through a graph, offering a comprehensive perspective on the evolving dynamics of the motor-scooter’s journey.
