A train goes into a tunnel at 20 m s1 and emerges from it at 55 m s1. The tunnel is 1500 m long. Assuming constant acceleration, find how long the train is in the tunnel for, and the acceleration of the train.

Title: Tunnel Odyssey: Unveiling Train Acceleration

---

Introduction: Embarking on a tunnel journey, a train gracefully transitions from one speed to another, threading through the tunnel’s mysterious expanse. This numerical exploration unveils the secrets of the train’s acceleration, shedding light on the time spent within the tunnel and the acceleration it undergoes.

Scenario Overview: Picture a train gracefully entering a tunnel with an initial velocity and emerging with an increased speed. This scenario encapsulates the essence of the train’s acceleration, a phenomenon we seek to dissect and understand in this numerical investigation.

Objectives:

1. Determine the time the train spends within the tunnel.
2. Calculate the acceleration experienced by the train during its tunnel passage.

Mathematical Analysis:

1. Time in Tunnel: Utilizing the kinematic equation �=�+��v=u+at, where: �v = final velocity (55 m/s), �u = initial velocity (20 m/s), �a = acceleration, �t = time in the tunnel.The equation can be rearranged as �=�−��t=av−u​.
2. Acceleration Calculation: The kinematic equation �2=�2+2��v2=u2+2as can be employed, where: �v = final velocity (55 m/s), �u = initial velocity (20 m/s), �a = acceleration, �s = displacement (1500 m).Solving for �a, we get �=�2−�22�a=2sv2−u2​.

Douglas Quadling Mechanics1 Exercise1C Q2

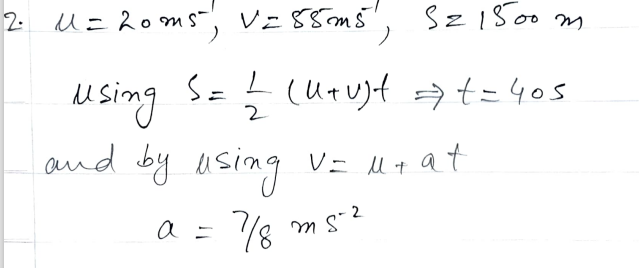
Conclusion:

This exploration ventures into the realm of train dynamics within a tunnel, unraveling the temporal and accelerative dimensions of its journey. By numerically dissecting the time spent in the tunnel and the acceleration experienced, we gain a deeper understanding of the intricate interplay between speed, time, and distance in the train’s tunnel odyssey.